用於解決一系列同餘方程組的問題。
《孫子算經》卷下第二十六題,叫做「物不知數」問題,原文如下:
有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二。問物幾何?
也就是,一個整數除以三餘二,除以五餘三,除以七餘二,求這個整數。
等下的解法步驟就會解以這個為例。
x ≡ a₁ (mod m₁)
x ≡ a₂ (mod m₂)
...
x ≡ aₖ (mod mₖ)
其中 m₁, m₂, ..., mₖ 是兩兩互質的正整數。
那麼,這個方程組在模 M = m₁ * m₂ * ... * mₖ 的範圍內有唯一解。
解法步驟:
計算 M = m₁ * m₂ * ... * mₖ
對於每個方程,計算 Mᵢ = M / mᵢ
找到 Mᵢ 在模 mᵢ 下的逆元 yᵢ,即 Mᵢ * yᵢ ≡ 1 (mod mᵢ)
解是 x = (a₁ * M₁ * y₁ + a₂ * M₂ * y₂ + ... + aₖ * Mₖ * yₖ) mod M
假設我們要找一個數 x,滿足:
x ≡ 2 (mod 3)
x ≡ 3 (mod 5)
x ≡ 2 (mod 7)
步驟 1:
M = 3 * 5 * 7 = 105
步驟 2:
M₁ = 105 / 3 = 35
M₂ = 105 / 5 = 21
M₃ = 105 / 7 = 15
步驟 3:
35 * 2 ≡ 1 (mod 3), 所以 y₁ = 2
21 * 1 ≡ 1 (mod 5), 所以 y₂ = 1
15 * 1 ≡ 1 (mod 7), 所以 y₃ = 1
步驟 4:
x = (2 * 35 * 2 + 3 * 21 * 1 + 2 * 15 * 1) mod 105
= (140 + 63 + 30) mod 105
= 233 mod 105
= 23
詳細原理解釋與反證明:
a) 對於任意 j ≠ i,Mⱼ 是 mᵢ 的倍數(因為 Mⱼ 包含了除 mⱼ 外的所有 m)。
所以 Mⱼ ≡ 0 (mod mᵢ) 當 j ≠ i。
b) Mᵢ * yᵢ ≡ 1 (mod mᵢ),這是逆元的定義。
c) 因此,當我們對 mᵢ 取模時,除了第 i 項外,其他所有項都變為 0:
x ≡ (0 + ... + 0 + aᵢ * Mᵢ * yᵢ + 0 + ... + 0) (mod mᵢ)
≡ aᵢ * (Mᵢ * yᵢ) (mod mᵢ)
≡ aᵢ * 1 (mod mᵢ)
≡ aᵢ (mod mᵢ)
這就證明了我們所得的解確實滿足所有的同餘方程。

https://cryptohack.org/courses/modular/crt1/
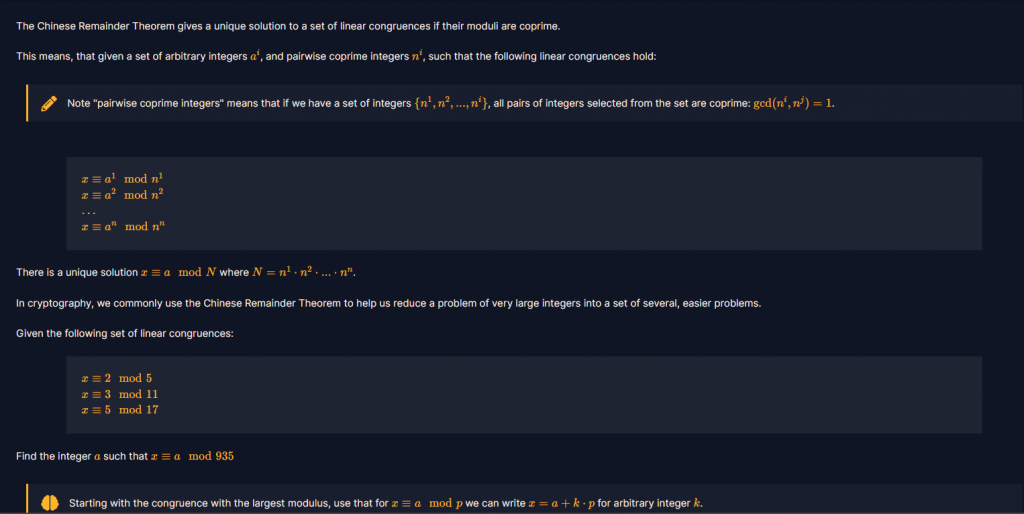
介紹中國餘式定理求解,並告訴我們,可以從模數最大的同餘式開始,利用任意整數k,將x表示為x = a + kp的形式。
題目要我們找出一個整數x,使得x除以5餘2,除以11餘3,除以17餘5。
而我們要返回滿足下面這個式子的 a:
x ≡ a mod 935(題目要我們求出a)
根據中國餘式定理的解題步驟,寫成python code,最後再返回 x % 935 的值。
a = [2, 3, 5] # 給定的餘數列表
n = [5, 11, 17] # 給定的模數列表
M = 1 # 初始化 M 為 1,M 將是所有模數的乘積
# 計算 M,M = m₁ * m₂ * ... * mₖ
for num in n:
M *= num
# 計算每個 Mi,Mi = M / mi
Mi = [M // N for N in n]
# 初始化 y 為 0 的列表,將用來存放每個 Mi 的逆元
y = [0] * len(Mi)
x = 0
# 計算每個方程的解並累加到 x
for i in range(len(Mi)):
y[i] = pow(Mi[i], -1, n[i]) # 計算 Mi 在模 n[i] 下的逆元 y[i]
x += a[i] * Mi[i] * y[i] # 累加每個方程的解到 x
x %= M
print(x % 935)
872
中國餘式定理:
今天查了中國餘式定理的相關資料,了解其解題步驟後也動手寫程式解題,收穫滿滿的一天(累死我了)。
